Phosphorus Loading and Westslope Cutthroat Trout
mbakken
View all records in the stressor response library
Species Common Name
Westslope Cutthroat Trout
Latin Name (Genus species)
Oncorhynchus clarkii lewisi
Stressor Name
Phosphorus loading
Specific Stressor Metric
Potential phosphorus loading
Stressor Units
tonnes/ha/year
Vital Rate (Process)
System capacity
Geography
Alberta foothills watersheds, excluding National Parks
Detailed SR Function Description
Phosphorus is a major driver of primary production in aquatic ecosystems that affects other biotic and abiotic factors. Low-level inputs of phosphorus during oligotrophic stream fertilization projects in B.C. have resulted in increased fish size and abundance due to substantial increases in trophic productivity with limited impact to water quality (Koning et al. 1998). However, higher levels of nutrient inputs lead to stream eutrophication and degraded water quality, including reduced nocturnal dissolved oxygen in summer (Chung 2013; Jacobsen and Marin 2008) and overall anoxic conditions that can impair biodiversity (Meijering 1991). For example, degraded stream habitats and fish winterkill conditions in Alberta foothills were correlated with theoretical increases in phosphorus runoff due to land use at the watershed scale (Norris 2012).
The phosphorus stressor-response curve was developed using potential phosphorous loading estimates and current FSA risk categories for the three native trout species trout (see MacPherson et al. 2019; AEP 2013). FSA risk categories vary from 0 (functionally extirpated) to 5 (very low risk). The potential phosphorous loading estimate for each watershed was obtained using ALCES© online. Phosphorus runoff was measured as a potential loading value for each watershed (tonnes/ha/year).
The stressor-response curve was derived by: a) using logistic regression to develop a statistical model relating probability of being within a given FSA category to the log-transformed phosphorous loading estimate; and, b) converting this statistical model into a stressor-response curve relating phosphorus to a percent reduction native trout system capacity from a pristine reference condition. Proportional-odds logistic regression was used since the response variable is a multinomial ordered variable (Venables and Ripley 2002). The proportional-odds assumption of independence among adjacent categories was assessed by comparing similarity of odds ratios among successive categories (Venables and Ripley 2002).
The stressor-response curve was derived from the proportional-odds logistic-regression models by estimating phosphorous loading estimates required for a 90% probability of falling within a given FSA category. This is similar logic to quantile regression (Cade and Noon 2003) that recognizes numerous unaccounted factors can be driving a response variable. FSA categories were converted to percent of reference condition using population percentages at transition points between adjacent FSA categories.
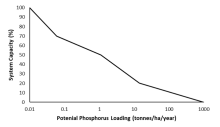
The FSA risk category for trout was rarely 3 or better when phosphorus loading potential was ≥0.1 tonnes/ha/year. No watersheds with a FSA risk category of 5 were observed. There was a significant phosphorus level effect (slope = -0.42, 95% profile confidence interval -0.65 to -0.21) with the probability of a watershed being within a lower FSA category increasing with phosphorus loading. From these probability distributions, the stressor-response for system capacity for the 3 native trout species at a given phosphorus loading estimate was developed (Figure 1).
A major issue in assessing the importance of potential stressors in driving a response variable is collinearity amongst different stressors (Zuur et al. 2010). If different stressors are highly correlated, it is impossible to distinguish relative importance without further experimentation. There was a high degree of correlation between potential phosphorus loading (tonnes/ha/year) and the relative sediment increase across the 73 watersheds (Pearson R = 0.62, 95% confidence interval 0.45 – 0.74). Thus, it was difficult using the available data to separate the importance of phosphorus or sediment independently on system capacity. Our approach was to create two separate stressor-response curves (i.e., one for potential phosphorus loading independent of the sediment index and vice-versa) and acknowledge that the observed response could be driven by the other stressor. As the Joe model accumulates cumulative effects multiplicatively (additive on a proportional scale), treating these two curves separately would inappropriately overemphasize the expected response. To overcome this issue, we treated sediment and phosphorus in the Joe model using a limiting factor approach. Simply, only the strongest, negative response from either the phosphorus or sediment stressor-response curves is used to calculate final system capacity. Anytime a watershed shows either phosphorus or sediment to be a hypothesized key driver, it must be acknowledged that the other stressor (i.e., sediment or phosphorus, respectively) could be the driver given the collinearity.
The phosphorus stressor-response curve was developed using potential phosphorous loading estimates and current FSA risk categories for the three native trout species trout (see MacPherson et al. 2019; AEP 2013). FSA risk categories vary from 0 (functionally extirpated) to 5 (very low risk). The potential phosphorous loading estimate for each watershed was obtained using ALCES© online. Phosphorus runoff was measured as a potential loading value for each watershed (tonnes/ha/year).
The stressor-response curve was derived by: a) using logistic regression to develop a statistical model relating probability of being within a given FSA category to the log-transformed phosphorous loading estimate; and, b) converting this statistical model into a stressor-response curve relating phosphorus to a percent reduction native trout system capacity from a pristine reference condition. Proportional-odds logistic regression was used since the response variable is a multinomial ordered variable (Venables and Ripley 2002). The proportional-odds assumption of independence among adjacent categories was assessed by comparing similarity of odds ratios among successive categories (Venables and Ripley 2002).
The stressor-response curve was derived from the proportional-odds logistic-regression models by estimating phosphorous loading estimates required for a 90% probability of falling within a given FSA category. This is similar logic to quantile regression (Cade and Noon 2003) that recognizes numerous unaccounted factors can be driving a response variable. FSA categories were converted to percent of reference condition using population percentages at transition points between adjacent FSA categories.
The FSA risk category for trout was rarely 3 or better when phosphorus loading potential was ≥0.1 tonnes/ha/year. No watersheds with a FSA risk category of 5 were observed. There was a significant phosphorus level effect (slope = -0.42, 95% profile confidence interval -0.65 to -0.21) with the probability of a watershed being within a lower FSA category increasing with phosphorus loading. From these probability distributions, the stressor-response for system capacity for the 3 native trout species at a given phosphorus loading estimate was developed (Figure 1).
A major issue in assessing the importance of potential stressors in driving a response variable is collinearity amongst different stressors (Zuur et al. 2010). If different stressors are highly correlated, it is impossible to distinguish relative importance without further experimentation. There was a high degree of correlation between potential phosphorus loading (tonnes/ha/year) and the relative sediment increase across the 73 watersheds (Pearson R = 0.62, 95% confidence interval 0.45 – 0.74). Thus, it was difficult using the available data to separate the importance of phosphorus or sediment independently on system capacity. Our approach was to create two separate stressor-response curves (i.e., one for potential phosphorus loading independent of the sediment index and vice-versa) and acknowledge that the observed response could be driven by the other stressor. As the Joe model accumulates cumulative effects multiplicatively (additive on a proportional scale), treating these two curves separately would inappropriately overemphasize the expected response. To overcome this issue, we treated sediment and phosphorus in the Joe model using a limiting factor approach. Simply, only the strongest, negative response from either the phosphorus or sediment stressor-response curves is used to calculate final system capacity. Anytime a watershed shows either phosphorus or sediment to be a hypothesized key driver, it must be acknowledged that the other stressor (i.e., sediment or phosphorus, respectively) could be the driver given the collinearity.
Function Derivation
Landscape correlation
Transferability of Function
This function was applied to the three species for which it was developed (Bull Trout, Athabasca Rainbow Trout, and Westslope Cutthroat Trout) within the Alberta range. While phosphorus loading has been shown to influence many aquatic systems, this function should be applied to other species with caution.
Source of stressor Data
Total expected phosphorus export was calculated following the Event Mean Concentration method described in Donahue (2013) and is based on land cover type and annual precipitation within the natural region. Phosphorous runoff values were obtained from the Upper Bow River Basin Cumulative Effects Study (ALCES Group, 2012) and phosphorous delivery coefficients were obtained from Stelfox et al. (2008). Total estimated phosphorous export was calculated in ALCES Online© based on 2010 footprint within the spatial unit of interest.
Function Type
continuous
Stressor Scale
log
References Cited
Government of Alberta. 2024. Phosphorus loading stressor-response function for Athabasca Rainbow Trout, Westslope Cutthroat Trout, and Bull Trout. Environment and Protected Area Native Trout Cumulative Effects Model.
Alberta Environment and Parks (AEP). 2013. Bull Trout Fish Sustainability Index. Alberta Fish and Wildlife Policy Branch, Edmonton, Alberta. https://www.alberta.ca/bull-trout-fsi.
ALCES 2012. Upper Bow River Basin Cumulative Effects Study. Report for Action for Agriculture, Alberta. 100 pp.
Cade, B.S. and B.R. Noon. 2003. A gentle introduction to quantile regression for ecologists. Frontiers in Ecology and the Environment 1: 412–420.
Chung, C. 2013. Diel oxygen cycles in the Bow River: Relationships to Calgary's urban nutrient footprint and periphyton and macrophyte biomass. MSc Thesis, University of Calgary, AB. 92 pp.
Donahue, W.F. 2013. Determining Appropriate Nutrient and Sediment Loading Coefficients for Modelling Effects of Changes in Landuse and Landcover in Alberta Watersheds. Water Matters Society of Alberta, Canmore, AB. 52pp.
Jacobsen, D., and R. Marin. 2008. Bolivian Altiplano streams with low richness of macroinvertebrates and large diel fluctuations in temperature and oxygen. Aquatic Ecology 42:643-656.
Koning, C., K. Ashley, P. Slaney, and A. Paul. 1998. Stream fertilization as a fisheries mitigation technique for perturbated oligotrophic trout streams in British Columbia. Pages 109-120 in M.K. Brewin and D.M.A. Monita, tech. Cords. Forest-fish conference: land management practices affecting aquatic ecosystems. Proc. Forest-Fish Conf., May 1-4, 1996, Calgary, AB. Nat. Resource Canada, Edmonton, AB, Inf. Rep. NOR-X-356.
MacPherson, L.M., M.G. Sullivan, A.L. Foote and C.E. Stevens. 2012. Effects of culverts on stream fish assemblages in the Alberta foothills. North American Journal of Fisheries Management 32: 480–490.
Meijering, M.P.D. 1991. Lack of oxygen and low pH as limiting factors for Gammarus in Hessian brooks and rivers. Hydrobiologia 223:159-169.
Alberta Environment and Parks (AEP). 2013. Bull Trout Fish Sustainability Index. Alberta Fish and Wildlife Policy Branch, Edmonton, Alberta. https://www.alberta.ca/bull-trout-fsi.
ALCES 2012. Upper Bow River Basin Cumulative Effects Study. Report for Action for Agriculture, Alberta. 100 pp.
Cade, B.S. and B.R. Noon. 2003. A gentle introduction to quantile regression for ecologists. Frontiers in Ecology and the Environment 1: 412–420.
Chung, C. 2013. Diel oxygen cycles in the Bow River: Relationships to Calgary's urban nutrient footprint and periphyton and macrophyte biomass. MSc Thesis, University of Calgary, AB. 92 pp.
Donahue, W.F. 2013. Determining Appropriate Nutrient and Sediment Loading Coefficients for Modelling Effects of Changes in Landuse and Landcover in Alberta Watersheds. Water Matters Society of Alberta, Canmore, AB. 52pp.
Jacobsen, D., and R. Marin. 2008. Bolivian Altiplano streams with low richness of macroinvertebrates and large diel fluctuations in temperature and oxygen. Aquatic Ecology 42:643-656.
Koning, C., K. Ashley, P. Slaney, and A. Paul. 1998. Stream fertilization as a fisheries mitigation technique for perturbated oligotrophic trout streams in British Columbia. Pages 109-120 in M.K. Brewin and D.M.A. Monita, tech. Cords. Forest-fish conference: land management practices affecting aquatic ecosystems. Proc. Forest-Fish Conf., May 1-4, 1996, Calgary, AB. Nat. Resource Canada, Edmonton, AB, Inf. Rep. NOR-X-356.
MacPherson, L.M., M.G. Sullivan, A.L. Foote and C.E. Stevens. 2012. Effects of culverts on stream fish assemblages in the Alberta foothills. North American Journal of Fisheries Management 32: 480–490.
Meijering, M.P.D. 1991. Lack of oxygen and low pH as limiting factors for Gammarus in Hessian brooks and rivers. Hydrobiologia 223:159-169.
File Upload
Stressor Response csv data
Data_WSCT_phosphorus.csv
(157 bytes)
| Phosphorus (tonnes/ha/year) | Mean System Capacity (%) | SD | low.limit | up.limit |
|---|---|---|---|---|
| 0.01 | 100 | 0 | 0 | 100 |
| 0.06 | 70 | 0 | 0 | 100 |
| 1.1 | 50 | 0 | 0 | 100 |
| 14.2 | 20 | 0 | 0 | 100 |
| 978 | 0 | 0 | 0 | 100 |
Stressor Response Chart